上個月被派了幾個工項,
其中一個是解我們開單員拍到的車牌照片。
前陣子在咱們一群影像愛好者的群組開始流傳一套程式,
一套號稱能檢測愛情動作片封面詐欺的程式!
什麼?天底下有這等好事?
於是我找到了開發這套程式的仁兄要到了原始論文,
認為他實現得不夠完美,間接促使我完成這項服務。
這篇文章可以幫你得出一個修圖參考值
(但某些情況不適用,文後會補充說明。)
接著會介紹論文以及背後數學原理,
對於檢測服務比較有興趣可以直接跳到後面。
原理
本文是 Analyzing Benford’s Law’s Powerful Applications in Image Forensics 這篇論文的延伸應用:
要講解這篇論文就要先解釋什麼是 Benford’s Law?
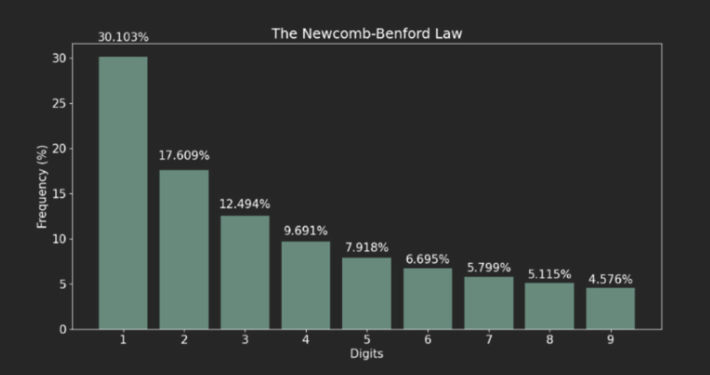
Benford’s Law 的概念就是人類世界中隨機數其實並不隨機,
其中數據的首位數字是遵循某種規律,這個規律就是 Benford’s Law。
Benford’s Law 公式:
$F_a = log_{10}{(frac{a+1}{a})}$, for all a = 1,2,…,9
這樣算起來會呈現由首位數字出現比率是 1 往 9 遞減的一個分佈:
舉個 Benford’s Law 的例子,
如果他們沒有說謊的話,這一萬人的存款首位數字應該會符合 Benford’s Law。
而論文本意是拿這個結論做二次壓縮來估測 JPEG 的壓縮率,
有興趣的大家可以自己閱讀一下論文。
實作
身為一個影像從業者,
一定要做到比內建函式庫快!
俗話說得好:
要看一個人會不會做立委,就要看他怎麼做立委。
我是說要加速就要從數學看起,所以讓我們來看一下公式:
其中 $D(i, j)$ 是轉換後的值,$i, j$ 是位置參數;
$f(x, y)$ 是原始圖片的亮度值,$x, y$ 也是位置參數。
發現亮度值可以提出來,其中位置參數可以自己組一個矩陣相乘,
我們暫且把包含所有 $i, j$ 組合的稱為母矩陣。
這個母矩陣可以重複用,就不用每個區塊都要算。
(原始圖片會被 N*N 的小區塊分割,N 通常是 8。)
因為一組 $i, j$ 負責一組子矩陣,
所以如果輸出入尺寸相同,母矩陣大小為: $N * N * N * N$
於是我用這方法寫了一個 Mask 法,
的確速度與 OpenCV 內置函數比肩了,但是還沒有超越(#。
再加速
於是我又對平行運算生起了一絲邪念,
如果我宣告一組共享記憶體紀錄首位數字,
並對計算每個區塊的計算採取平行運算呢?
起初我是用 Lock 方法,後來發現這樣設計寫入的時候會有 Race Condition 問題,
後來便採取 Lock free 實作,缺點是佔用的記憶體較多。
數據判讀
目前線上提供服務的機器人都是使用 DownSample 方法做計算。
特別需要說明的是手機原生相機就會做白平衡、明暗部校正,
尤其是 iPhone 做得非常優秀。
開源
原始論文使用 Uncompressed Colour Image Database 資料庫,
探討使用原始無損圖片如何估計 JPEG 壓縮率,
所以本文的物理意義是估算原始無損圖片與輸入圖片的差異度。
本文估計值僅供參考,
窮盡科技之力後不如鼓起勇氣約網戀對象出來走走!
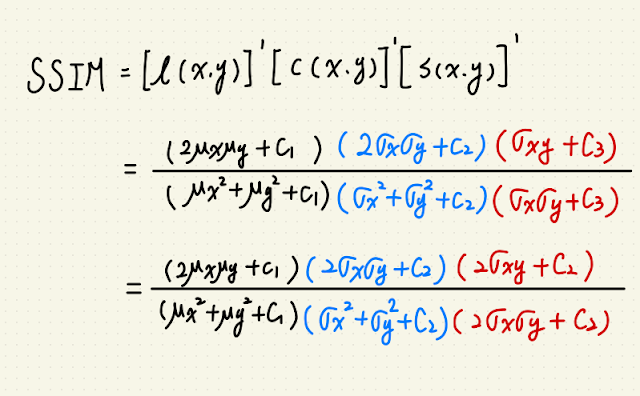
這篇是 SSIM 系列第三篇,接續前篇 使用 PyTorch 實做 2D 影像捲積,
要來談一下 SSIM 如何在不均勻光源下優化 SSIM。
如果你是剛開始接觸 SSIM 的人,可能會跟我一樣看過一篇幫愛因斯坦去噪的實現文章。
沒錯,當初我也是看到愛因斯坦的臉逐漸浮現,才覺得 SSIM 可以拿來解工程問題!
只是愛因斯坦那篇的調節亮度方法對於工程來說太過理想化,
問題在於他是把整張圖片的像素值乘以 0.9 調亮度!
這樣的話 SSIM 算法裡面的變異數項是不會變的,只有考慮到平均數項,
所以他做出來的 SSIM 值不會差太多。
但是現實世界是很絢爛多彩且難以預測的,
就像我前兩天載室友出門,停等紅燈時他突然發生奇怪的聲音,
轉頭問他在幹麻?
:我在跟你的機車排氣管對頻。
實務上,我們可能會面對不均勻光源的問題,就像是街邊的燈光:
這燈光很糟糕,比忘記簽聯絡簿的國小學童還糟糕,
因為它的光源只會影響照片的一部分,而且還會隨著距離遞減。
如果使用原版的 SSIM 方法對比這種有無開燈的照片,
則 SSIM值會不可避免的大幅下降,
但這兩張照片的前景內容物(e.g. 人、車、直升機、脫光衣服在路上奔跑的人)一樣對吧?
所以在基於前景的情況下,有些時候我們會希望有無開燈的照片應該要一樣,
數學上也就是得到理想值為 1 的 SSIM 值。
(實在是繞口令,讓我想到事件攝影機。)
要解這個問題就要先了解 SSIM 的本質,
SSIM 是由 sliding window 來解圖片中各自區域均值、變異數,還有兩張圖片的共變數所構成。
而二維的 window 又是由一維的 kernel (通常是 Gaussian)矩陣相乘得到,
基本上 OpenCV 裡面提供的方法是這樣:
nkernel = cv2.getGaussianKernel(11, 1.5)
nwindow = np.outer(nkernel, nkernel.transpose())
往 cv2.getGaussianKernel 裡面看,我們可以知道這條函式來自 getGaussianKernelBitExact:
再往 getGaussianKernelBitExact 裡面看:
重點是 158, 181 行運算的兩個迴圈,他們在幫忙算高斯核並歸一化。
我們的重點是歸一化,以前的簡易版 OpenCV Source Code 大概長這樣:
def getGaussianKernel(M, std):
n = np.arange(0, M) - (M - 1.0) / 2.0
sig2 = 2 * std * std
w = np.exp(-n ** 2 / sig2)
muli = 1/sum(w[:])
wn = w * muli
return wn
這種歸一化的一維高斯核長得像是:
扁扁有點可愛,像是軟趴趴的史萊姆。
但是這樣可能會造成一些問題,
讓我們看看非歸一化的原始高斯核:
def ourGaussianKernel(M, std):
n = np.arange(0, M) - (M - 1.0) / 2.0
sig2 = 2 * std * std
w = np.exp(-n ** 2 / sig2)
# muli = 1/sum(w[:])
# wn = w * muli
return w
def ssim_Normalized(img1, img2):
C1 = (0.01 * 255)**2
C2 = (0.03 * 255)**2
img1 = img1.astype(np.float64)
img2 = img2.astype(np.float64)
nkernel = cv2.getGaussianKernel(11, 1.5)
nwindow = np.outer(nkernel, nkernel.transpose())
nmu1 = cv2.filter2D(img1, -1, nwindow)[5:-5, 5:-5]
nmu2 = cv2.filter2D(img2, -1, nwindow)[5:-5, 5:-5]
nmu1_sq = nmu1**2
nmu2_sq = nmu2**2
nmu1_mu2 = nmu1 * nmu2
nsigma1_sq = cv2.filter2D(img1**2, -1, nwindow)[5:-5, 5:-5] - nmu1_sq
nsigma2_sq = cv2.filter2D(img2**2, -1, nwindow)[5:-5, 5:-5] - nmu2_sq
nsigma12 = cv2.filter2D(img1 * img2, -1, nwindow)[5:-5, 5:-5] - nmu1_mu2
nssim_map = ((2 * nmu1_mu2 + C1) *
(2 * nsigma12 + C2)) / ((nmu1_sq + nmu2_sq + C1) *
(nsigma1_sq + nsigma2_sq + C2))
return nssim_map.mean()
def ssim_Unnormalized(img1, img2):
C1 = (0.01 * 255)**2
C2 = (0.03 * 255)**2
img1 = img1.astype(np.float64)
img2 = img2.astype(np.float64)
kernel = ourGaussianKernel(11, 1.5)
window = np.outer(kernel, kernel.transpose())
mu1 = cv2.filter2D(img1, -1, window)[5:-5, 5:-5]
mu2 = cv2.filter2D(img2, -1, window)[5:-5, 5:-5]
mu1_sq = mu1**2
mu2_sq = mu2**2
mu1_mu2 = mu1 * mu2
sigma1_sq = cv2.filter2D(img1**2, -1, window)[5:-5, 5:-5] - mu1_sq
sigma2_sq = cv2.filter2D(img2**2, -1, window)[5:-5, 5:-5] - mu2_sq
sigma12 = cv2.filter2D(img1 * img2, -1, window)[5:-5, 5:-5] - mu1_mu2
ssim_map = ((2 * mu1_mu2 + C1) *
(2 * sigma12 + C2)) / ((mu1_sq + mu2_sq + C1) *
(sigma1_sq + sigma2_sq + C2))
return ssim_map.mean()
if __name__=='__main__':
img1_path = 'img1.png'
img2_path = 'img2.png'
kernelSize = 21
light = list(map(np.uint8, gkern(kernlen=kernelSize, std=1.5)*100))
img1 = np.random.randint(0, 150, size=(100, 100)).astype(np.uint8)
img2 = np.zeros_like(img1)
img2[:] = img1[:]
row = np.random.randint(int(kernelSize/2), img1.shape[0] - int(kernelSize/2))
col = np.random.randint(int(kernelSize/2), img1.shape[1] - int(kernelSize/2))
times = np.random.randint(1, 100)
for i in range(0, times):
img2[row:row + kernelSize, col:col + kernelSize] += light
img2 = np.clip(img2, 0, 255)
print("This is Normalized): " + str("{:.5f}".format(ssim_Normalized(img1, img2))))
print("This is Unnormalized): " + str("{:.5f}".format(ssim_Unnormalized(img1, img2))))
親測可用:
繼 200. Number of Islands 後,又遇到一個影像處理的問題。
這題要用動態規劃來解,菜雞如我第一時間沒想到動態規劃,
但是後來也自己解出來了,紀錄一下我的解題心路歷程。
題目簡介:
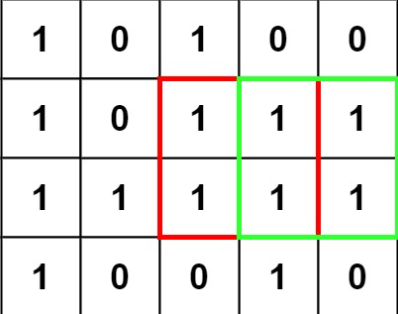
給你一張尺寸為 m x n 像素且只包含(0,1)的圖片稱為 Matrix ,
其中 1 代表有像素的區域,找出此張圖片中含有 1 的最大正方形區域面積。
第一階段想法:循序檢測法
把每個點都當作候選正方形的左上角,
先求 Row 再驗證每個 Col 是否符合正方形區域預想?
若有,就回傳正方形區域面積;
若無,就回傳 0。
假設圖片中有 N 個元素,這個想法的時間複雜度為:
$$O(N^{2})$$
但是我們會遇到一個特殊情況,當最大正方形在驗證失敗的候選正方形的的情況,
像是:
就很尷尬,其中 $$S_m$$ 不等於 6 的原因是本圖中最大正方形是交由 min(m, n) 決定,
所以不用檢查到 $$S_m = 6$$ 可以降低計算時間。
結果:Wrong Answer
第二階段:動態規劃法
所以我決定再不增加時間複雜度的情形下,由小到大、每個正方形都檢測。
使用動態規劃,每一步驟又拆成兩小步:
第一步:驗證對角線是否為 ‘1’ ?
第二步:驗證相應 X, Y軸是否為 ‘1’ ?
若有任一步檢測到 ‘0’ ,則回傳步數 S 的平方當作正方形面積。
不過鑑於這個作法時間複雜度遇到 Worst Case (全為 ‘1’ 的圖片時)仍為 $$O(N^{2})$$
結果:Time Limited Error
第三階段:利用影像(數據)特性降低時間複雜度。
問自己一個問題:最低滿足圖片中最大正方形的條件是什麼?
答案是任何大於(長/2)*(寬/2)的正方形,
因為本題目中不考慮重疊問題,所以用數學上來說:
一圖片尺寸為 m*n ,若有任意正方形面積大於(m/2 + k)(n/2 + k),
而 k 恆大於零的話,此正方形為圖片中最大的正方形就成立。
而候選次大正方形面積必定為(m/2 – k)(n/2 – k),
所以每個點出發後,
檢測 (m*n/4) + m + n – 1 個像素就知道這個正方形是不是最大的了。
結果:Accept
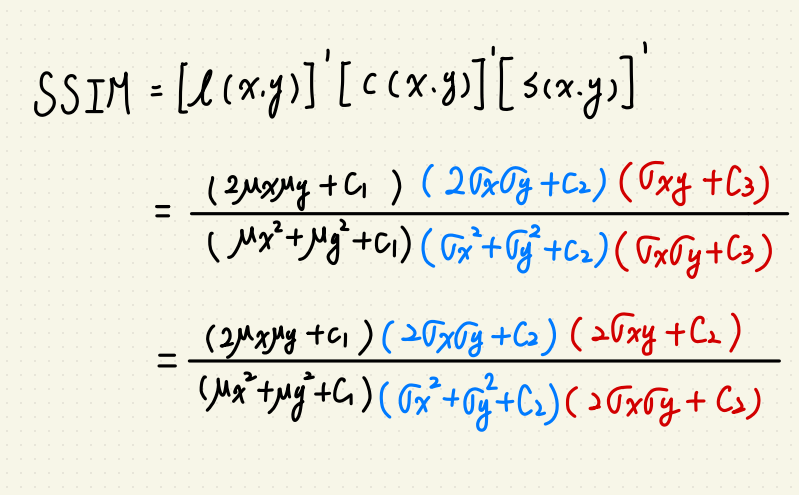
SSIM 是一種指標,用於比較兩張圖的相異程度。
指標主要參考三個面向:
$$l(xy) = frac{2mu_xmu_y+C1}{mu^2_xmu^2_y+C1}$$
$$c(xy) = frac{2sigma_xsigma_y+C2}{sigma^2_xsigma^2_y+C2}$$
$$s(xy) = frac{sigma_{xy}+C3}{sigma_xsigma_y+C3}$$
以上的 $$C1 = K_1l^2, C2 = K_2l^2,C3 的部份可以簡化為 C3 = frac{C2}{2}$$
$$k_1 = 0.01, k_2 = 0.03, l 則為圖片的灰度值。$$
整體的 SSIM 為三項相乘:
$$SSIM(x,y) = [l(x,y)]^alpha[c(x,y)]^beta[s(x,y)]^gamma$$
在這邊 $$alpha, beta, gamma $$ 都簡化為 1。
這樣我們就可以簡化 SSIM 為:
然後我看到其他人有用 Numpy 實現,
就想著是不是自己能寫一版 PyTorch 來用?
大概會遇到兩個問題:
1.手刻 Gaussian Kernel 要塞在哪?
2.轉換資料至 GPU 上的時候會有誤差。
第一個問題當然是不能用 torch.nn.Conv2d() 來解,
因為這個 API 不能自己定義 Kernel,而且我們不希望這個 Kernel 的權重跑掉。
(Doc在此)
所以我們要用 torch.nn.functional.conv2d
(Doc在此)
接著我們要手刻一下 Gaussian Kernel:
def gaussian_fn(M, std):
n = torch.arange(0, M) - (M - 1.0) / 2.0
sig2 = 2 * std * std
w = torch.exp(-n ** 2 / sig2)
return w
def gkern(kernlen=256, std=128):
"""Returns a 2D Gaussian kernel array."""
gkern1d = gaussian_fn(kernlen, std=std)
gkern2d = torch.outer(gkern1d, gkern1d)
return gkern2d
這個方法我是從這邊看來的,
簡單來說就是從 1d Gaussian 用矩陣乘法造 2d Gaussian。
把整體程式碼寫出來:
def gaussian_fn(M, std):
n = torch.arange(0, M) - (M - 1.0) / 2.0
sig2 = 2 * std * std
w = torch.exp(-n ** 2 / sig2)
return w
def gkern(kernlen=256, std=128):
"""Returns a 2D Gaussian kernel array."""
gkern1d = gaussian_fn(kernlen, std=std)
gkern2d = torch.outer(gkern1d, gkern1d)
return gkern2d
def ssim_torch(img1, img2, kernel_size=11):
start_time = time.time()
C1 = (0.01 * 255)**2
C2 = (0.03 * 255)**2
transf = transforms.ToTensor()
guassian_filter = gkern(kernel_size, std=1.5).expand(3, 1, kernel_size, kernel_size)
H, W, C = img1.shape[0], img1.shape[1], img1.shape[2]
img1, img2 = torch.from_numpy(img1), torch.from_numpy(img2)
img1B, img1G, img1R = img1[:,:,0], img1[:,:,1], img1[:,:,2]
img2B, img2G, img2R = img2[:,:,0], img2[:,:,1], img2[:,:,2]
img1B, img1G, img1R = img1B.unsqueeze(0), img1G.unsqueeze(0), img1R.unsqueeze(0)
img2B, img2G, img2R = img2B.unsqueeze(0), img2G.unsqueeze(0), img2R.unsqueeze(0)
img1 = torch.cat((img1B, img1G, img1R), dim=0).unsqueeze(0).float()
img2 = torch.cat((img2B, img2G, img2R), dim=0).unsqueeze(0).float()
mu1 = F.conv2d(img1, weight=guassian_filter, stride=1, groups=3)
mu2 = F.conv2d(img2, weight=guassian_filter, stride=1, groups=3)
mu1_sq = mu1**2
mu2_sq = mu2**2
mu1_mu2 = mu1 * mu2
sigma1_sq = F.conv2d(img1**2, weight=guassian_filter, stride=1, groups=3) - mu1_sq
sigma2_sq = F.conv2d(img2**2, weight=guassian_filter, stride=1, groups=3) - mu2_sq
sigma12 = F.conv2d(img1 * img2, weight=guassian_filter, stride=1, groups=3) - mu1_mu2
ssim_map = ((2 * mu1_mu2 + C1) *
(2 * sigma12 + C2)) / ((mu1_sq + mu2_sq + C1) *
(sigma1_sq + sigma2_sq + C2))
print("This is torch_SSIM computer time: " + "{:.3f}".format((time.time()-start_time)))
return ssim_map.mean().detach().numpy()
這邊的 sigma_sq 是先把元素數量 N 提出來,
看起來有點不直覺要想一下。
如果你跟我一樣追求效率,就會想把 tensor.Tensor 轉成 tensor.Tensor.cuda 拿來加速。
這樣會遇到兩個小問題:
第一個小問題應該是轉換時間差,
第二個問題應該是 CPU 轉 GPU 的 tensor Loss。
結論:
Ref.
https://stackoverflow.com/questions/60534909/gaussian-filter-in-pytorch
https://blog.csdn.net/a2824256/article/details/115013851
附上 Github Repo
如何對本文有任何疑問或書寫錯誤,
歡迎留言或是聯絡我:
wuyiulin@gmail.com
2023-11-13 分層捲積的更新
基於本部落格此篇文章的實現,
雖然寫得有點醜但親測可用!
快速排序算法擁有最佳計算複雜度 O(n log n),
但在特殊情況下會退化成 O(n^2)。
其中一個特殊情況就是大量重複元素的排列問題。
解決問題前,
先介紹快速排序法的實現。
假設你得到一隨機一維陣列要做升冪排序,
最終的結果需要是這樣:
選定隨機陣列最左側為 pivot ,pivot 為 L指標、最右側為 R指標。
首先先判斷終止條件:R 的 index 是否等於 L 的 index?
等於的話就將 pivot 的 值 與 R、L 的值交換,進行下一循環。
R 的 index 不等於 L 的 index的話繼續尋找:
R指標啟動尋找小於等於 pivot 的值,L 尋找大於 pivot 的值,找到就鎖定。
若 R 的 index != L 的 index,則兩者的值交換。
以此類推,當 R 的 index == L 的 index 時,交換 pivot 與 R 的值。
並以交換點為準,分割左邊右邊兩個子循環。
這邊可以順便推導為什麼 quick sort 的計算複雜度為 O(n log n),
因為相較於 bubble sort 中每個 pivot 要比較 n-1 個元素,
quick sort 在第二次以後的理想狀況每個 pivot 只需比較 (n/2)^m個元素
(m=排序次數-1)。
所以最佳計算複雜度才會是 O(n log n) // n個 pivot 乘上該次比較元素量。
但是齁,人算不如天算。
有時候就會遇到很棘手的情況,讓 quick sort 一點都不 quick。
主要分為兩種:
1.已排序數列。
沒有的話 L 先搜尋,分為三種情況:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <iostream<
#include <vector<
#include <algorithm<
#include <random<
void swap(int *array, int i, int j) {
array[i] = array[i] ^ array[j];
array[j] = array[i] ^ array[j];
array[i] = array[i] ^ array[j];
}
void quicksort(int *array, int left, int right) {
if (left >= right)
{
return;
}
int P = left;
int L = left;
int R = right;
while(L <= R)
{
if(nums[L] < nums[P])
{
swap(nums, L, P);
L++;
P++;
}
else if(nums[L] == nums[P])
{
L++;
}
else
{
if(nums[R] > nums[P])
{
R--;
}
else if(nums[R] == nums[P])
{
swap(nums, R, L);
swap(nums, L, P);
R--;
L++;
}
else
{
swap(nums, R, L);
swap(nums, L, P);
R--;
L++;
P++;
}
}
}
quicksort(nums, left, P-1);
quicksort(nums, P+1, right);
}
int main() {
int ARRAY_SIZE = 100;
int array[ARRAY_SIZE];
// 設定隨機種子
srand(time(0));
// 生成隨機一維陣列
for (int i = 0; i < ARRAY_SIZE; i++) {
array[i] = rand() % 11; // 生成 0 到 100 之間的隨機整數
}
printf("原始陣列:");
for (int j = 0; j < ARRAY_SIZE; j++) {
printf("%d ", array[j]);
}
printf("n");
quicksort(array, 0, ARRAY_SIZE - 1);
printf("排序後:");
for (int j = 0; j < ARRAY_SIZE; j++) {
printf("%d ", array[j]);
}
printf("n");
return 0;
}
好,大功告成!
你現在可以用 Quick Sort 面對多重複元素的排列問題了!
本文建議有點雲特徵的先驗知識者閱讀,
我會盡量講得平易近人,
但仍建議請先參考此篇,先了解基本點雲處理如何處理特徵。
這篇論文的重點在於改變了底層特徵方法。
論文中由這張圖來解釋:
因為現行解決 Rotation Invariant 的方法都是乘上一個矩陣去收集數據,
並沒有考慮點與點之間的結構關係(i.e.上圖笑臉)。
但是我覺得這個例子呈述得很容易誤導,
聽起來很像在解決高低解析度、上下採樣的問題,
實際上在點雲裡面應該是解決類似 KNN 特徵的問題才對。
像是那三個有黑色像素的點,間隔距離、彼此夾角之類的結構關係所產生的資訊。
作者認為現在的 CNN 都沒有抓到結構關係 (Pose) 的精華
(e.g. 點雲中點與點的區域關係 AKA 底層特徵),
所以要提出解決方法稱為 PaRI 的新架構來解決問題
(我猜是 Pose: Ambiguity-free 3D Rotation-invariant 的縮寫)。
舊有的底層特徵方法:
好,那要改進一定得知道改哪裡嘛?
之前別人是怎麼做這種結構特徵的?
答案是:Point Pair Feature(PPF)
 |
| Point Pair Peature |
Pr 是參考點,想像成 KNN 的目標點;
Pj 是 Pr 附近的鄰居點,有 K 個;
∂n_r 是相較於 r 的三維座標軸,用 gram-schmidt orthogonalization 算出來的,
忘記的同學可以去複習一下 GSO。
所以經過 PPF 計算,我們會得到一組四個特徵如下圖:
這樣會出個小問題,各位想想好的底層特徵應該要具備什麼特性?
應該要具備獨特性嘛!
因為這樣訓練起來才不會與其他特徵混淆。
仔細觀察 αn 的方程式我們會發現,沒有一條能分辨在這個半徑為 d 的圓圈上,
有若干個法向量相同的 Pj 的辦法。
(∂1_r, ∂1_j 分別代表各自的法向量,ModelNet40資料集會給定。)
改善方法:
在改善之前,我們先想想舊有方法遇到什麼問題?
問題是缺少 Pr 與 Pj 間的獨特特徵,對吧?
所以我們希望新的方法最好讓每個 Pj 對 Pr 有獨特性。
Local Reference Frame(LRF) + Augmented Point Pair Feature(APPF)
就能解決這個問題。
LRF
 |
| Local Reference Frame |
左邊那個飛機圖,是為了說明使用 Global Feature 會有問題而存在的,
有興趣可以深入論文研究。
LRF 這裡我們要先建三軸,首先要拿到 e^2_r;
e^2_r = Pr – mr 的座標向量,mr 是 Pj 們的重心。
接著根據公式建三軸:
APPF
 |
| Augmented Point Pair Feature |
接著把 d 投影到 π_d 上。
什麼?你說 π_d 是什麼?
論文這裡沒有寫得很清楚,
我也看了很久,最後是對照著官方程式碼看才看出來。
其實 π_d 就是座標向量 e^2_r!
投影上去,然後用 arctan 取角度回來。
不知道為什麼用 arctan 而不用 tan 的同學,這裡有兩個理由:
1.對應域
i.e. tan(45°) = 1 = tan(225°)
但是 arctan 只會給你 45°
2.極值
tan(89.9°) ≈ 5729.58,但 tan(90.1°) ≈ -5729.58。
arctan(5729.58) ≈ 89.9°,但 arctan(-5729.58) ≈ -90.1°。
以上。
若有任何錯誤請聯絡我xD
因為最近在解 Leetcode 的 91. Decode Ways,