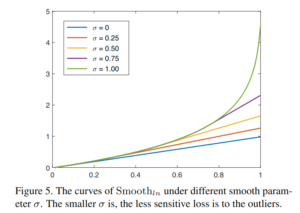
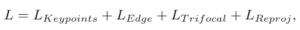最近上班遇到一些圖片顏色偏離原色,
身為影像工程從業者就會想自己寫 3A算法來校正。
而自動白平衡便是 3A 中的其中 1A – 南湖大山!
而自動白平衡便是 3A 中的其中 1A – Auto White Balance
自動白平衡的核心就是解決圖片色偏的方法,
大都是找到圖片中的參考值,
再用參考值及不同方法去對整張圖片做校正。
像是灰色世界算法就是拿全圖片的加總的三通道均值當作參考值,
再拿這個參考值除以三通道分別均值做成三通道的增益,
得到三通道增益後分別對通道相乘。
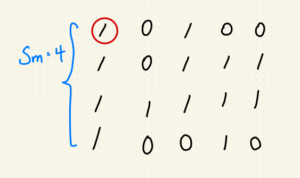
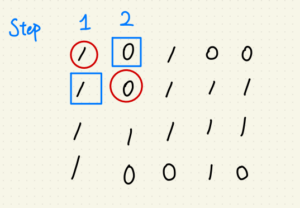
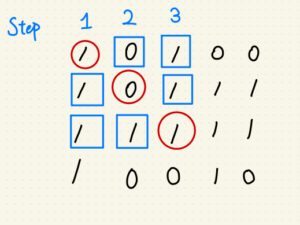
今天提到的完美反射核心,它的概念是相信圖片中有一群接近白色的區塊,
因為 RGB or BRG 的世界裡面 (255, 255, 255) 就是白色嘛,
所以有點像找到這塊邊長為 255 的正方形中那群最遠離原點 (0, 0, 0) 的那群點。
找到那群點後,再求得這群的均值作為參考值,
參考值除以各通道的均值就能得到各通道的增益,
最後再拉回去與原圖相乘 -> 結案。
def AutoWhiteBalance_PRA(imgPath, ratio=0.2): # 自動白平衡演算法_完美反射核心, 0 < ratio <1.
BGRimg = cv2.imread(imgPath)
BGRimg = BGRimg.astype(np.float32) # 將資料格式轉為 float32,避免 OpenCV 讀圖進來為 np.uint8 而造成後續截斷問題。
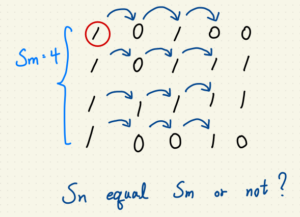
pixelSum = BGRimg[:,:,0] + BGRimg[:,:,1] + BGRimg[:,:,2]
pexelMax = np.max(BGRimg[:,:,:]) # 求三通道加總最大值作為像素值拉伸指標
row , col, chan = BGRimg.shape[0], BGRimg.shape[1], BGRimg.shape[2]
pixelSum = pixelSum.flatten()
imgFlatten = BGRimg.reshape(row*col, chan)
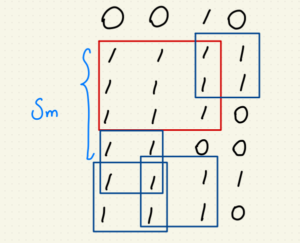
thresholdNum = int(ratio * row * col)
thresholdList = np.argpartition(pixelSum, kth=-thresholdNum, axis=None) # 由右至左設定閾值位置,並得到粗略排序後的索引表。
thresholdList = thresholdList[-thresholdNum:] # 取得索引表中比閾值大的索引號
blueMean, greenMean, redMean, i = 0, 0, 0, 0
for i in thresholdList:
blueMean += imgFlatten[i][0]
greenMean += imgFlatten[i][1]
redMean += imgFlatten[i][2]
blueMean /= thresholdNum
greenMean /= thresholdNum
redMean /= thresholdNum
blueGain = pexelMax / blueMean
greenGain = pexelMax / greenMean
redGain = pexelMax / redMean
BGRimg[:,:,0] = BGRimg[:,:,0] * blueGain
BGRimg[:,:,1] = BGRimg[:,:,1] * greenGain
BGRimg[:,:,2] = BGRimg[:,:,2] * redGain
BGRimg = np.clip(BGRimg, 0, 255)
BGRimg = BGRimg.astype(np.uint8)
return BGRimg
取值範圍直接變成 [0, 255]