繼 200. Number of Islands 後,又遇到一個影像處理的問題。
這題要用動態規劃來解,菜雞如我第一時間沒想到動態規劃,
但是後來也自己解出來了,紀錄一下我的解題心路歷程。
題目簡介:
給你一張尺寸為 m x n 像素且只包含(0,1)的圖片稱為 Matrix ,
其中 1 代表有像素的區域,找出此張圖片中含有 1 的最大正方形區域面積。
第一階段想法:循序檢測法
把每個點都當作候選正方形的左上角,
先求 Row 再驗證每個 Col 是否符合正方形區域預想?
若有,就回傳正方形區域面積;
若無,就回傳 0。
假設圖片中有 N 個元素,這個想法的時間複雜度為:
$$O(N^{2})$$
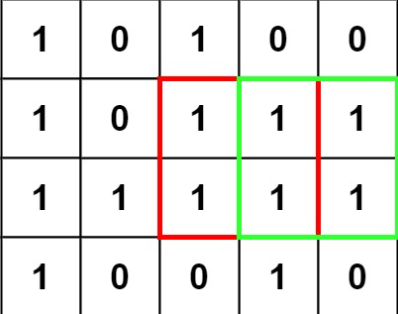
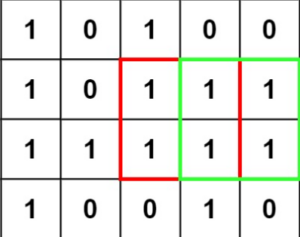
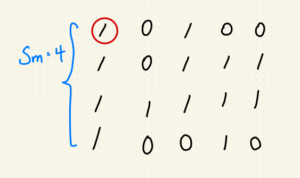
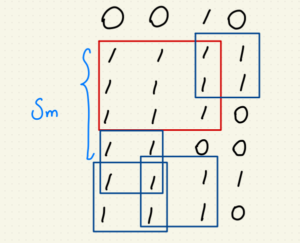
但是我們會遇到一個特殊情況,當最大正方形在驗證失敗的候選正方形的的情況,
像是:
就很尷尬,其中 $$S_m$$ 不等於 6 的原因是本圖中最大正方形是交由 min(m, n) 決定,
所以不用檢查到 $$S_m = 6$$ 可以降低計算時間。
結果:Wrong Answer
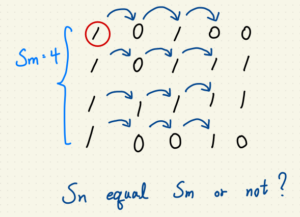
第二階段:動態規劃法
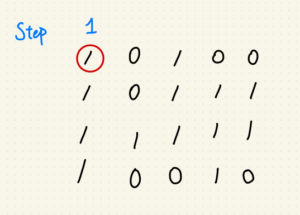
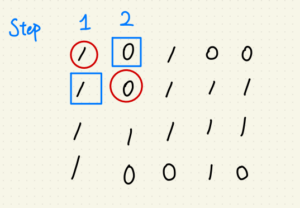
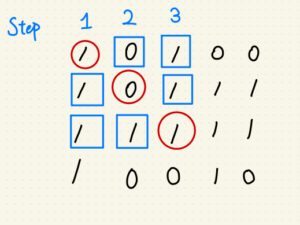
所以我決定再不增加時間複雜度的情形下,由小到大、每個正方形都檢測。
使用動態規劃,每一步驟又拆成兩小步:
第一步:驗證對角線是否為 ‘1’ ?
第二步:驗證相應 X, Y軸是否為 ‘1’ ?
若有任一步檢測到 ‘0’ ,則回傳步數 S 的平方當作正方形面積。
不過鑑於這個作法時間複雜度遇到 Worst Case (全為 ‘1’ 的圖片時)仍為 $$O(N^{2})$$
結果:Time Limited Error
第三階段:利用影像(數據)特性降低時間複雜度。
問自己一個問題:最低滿足圖片中最大正方形的條件是什麼?
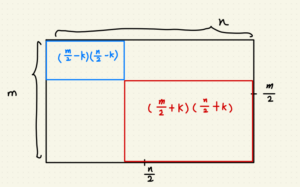
答案是任何大於(長/2)*(寬/2)的正方形,
因為本題目中不考慮重疊問題,所以用數學上來說:
一圖片尺寸為 m*n ,若有任意正方形面積大於(m/2 + k)(n/2 + k),
而 k 恆大於零的話,此正方形為圖片中最大的正方形就成立。
而候選次大正方形面積必定為(m/2 – k)(n/2 – k),
所以每個點出發後,
檢測 (m*n/4) + m + n – 1 個像素就知道這個正方形是不是最大的了。
結果:Accept