上個月被派了幾個工項,
其中一個是解我們開單員拍到的車牌照片。
由於我們開單員同仁都是阿伯阿桑,
基本上不太會用 PDA 拍照,所以拍回來的照片都歪歪的。
不太像場站固定機位會回傳的那樣方正,有時候還會有部份缺漏。
為了解這個問題,我去研究過阜爾(城市車旅)、普客(Times)還有一些第三方怎麼做的?
至少到 2024 年這個時間點,停車場業者主要都是控制他們的開單員要拍正,
據我所知沒有任何一間廠商對這點做妥善處理。
先限縮一下問題,因為特徵點根據不同狀況有不同參照物,
通常車牌特徵點都是用角點,所以先把特徵點設定為角點。
解這個問題的關鍵有三個:
第一個是角點濾波器,你要怎麼知道抓出來的特徵點是不是角點?
第二個是角點的順序,
角點順序對了,就能做些線性代數運算把車牌校正回來再送去 OCR。
第三個是角點的缺補,有時候缺了一點就不能把車牌校正回來。
或是你只有對角兩點,要怎麼把這些點補回來?
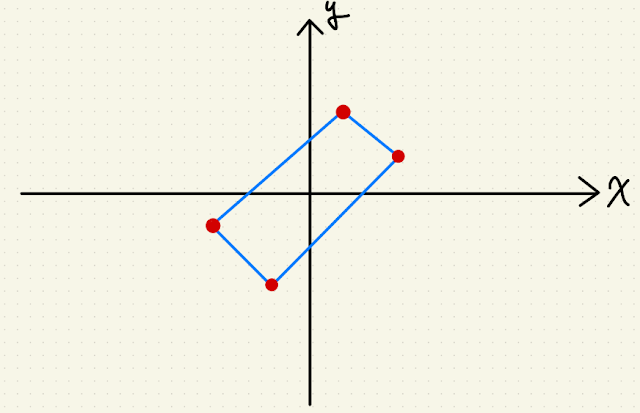
這篇分享很幸運的狀況 – 四個角點都抓到,只需求其順序:
我有看過幾種校正角點的方法,
比較主流且技術樓地板低的方法是訓練車牌校正模型,
餵一堆歪斜的車牌讓機器模型幫忙校正、得出被校正後的四點座標。
比較聰明一點的會用四象限去分點位,
但是四象限法會遇到一些問題像是:
有重複點在同一象限,你要怎麼辦?
要比 X 軸 還是比 Y軸?
答案是先看在哪個象限,再寫邏輯處理。
有些人會說:
用霍夫變換抓直線回來校正車牌,不就可以把車牌四點都分到獨立的象限嗎?
我當初也是這麼想的,
但實務上會被水箱護網、環境因素(排水溝蓋等)帶歪,
請記得我們不是在做機臺 AOI 那種環境相對單純的工作,所以霍夫變換的效果有限。
所以用四象限法不僅會面臨邏輯複雜,
如果加了霍夫變換,又需要面臨霍夫變換的不穩健性。
結論:你應該用更好的方法!
Ray Casting法
這套是我自己有天看到 Carmack 的德軍總部為了節省計算量時用了 Ray Casting 後,
被 Ray Casting 啟發想出來的。
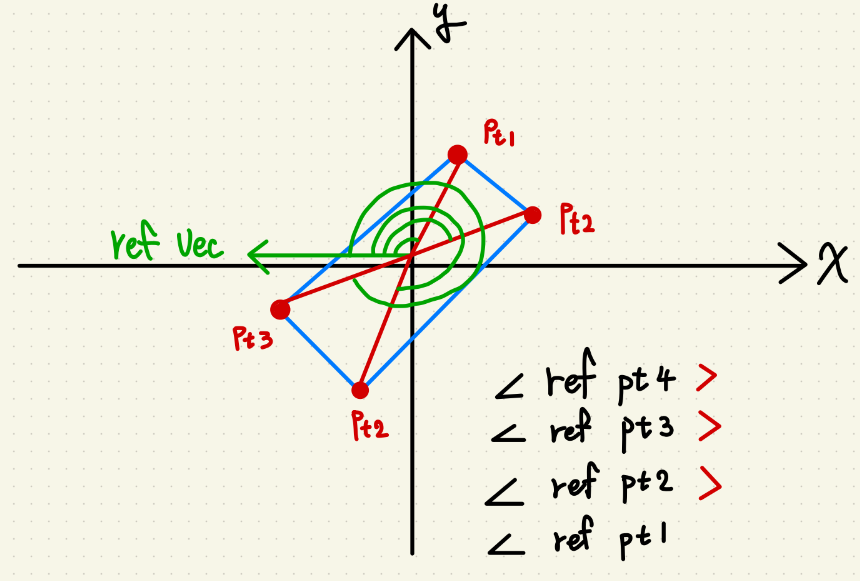
原理是利用任一從原點出發的向量,作為參考向量。
隨後計算每個點到原點的向量,稱為特徵向量,
將特徵向量與標準向量做 COS 值並計算角度,
為了保證角度要是同一個順序(順逆時鐘)求出來的,
最後記得看一下 COS 值正負做處理。
這套的好處相比於前述方法有三個:
1.是根據物理原理,這個順序一定是對的,
2.少去複雜的邏輯設計,程式碼易讀易於維護。
3.N個點的 Case 只須計算 N次,計算複雜度低。
 |
| Ray Casting 法 |
最後埋個彩蛋,參考向量設{-1, 0}能有效降低實務上的計算複雜度,
歡迎同行交流。
以上。
Please feel free to contact me if you have any questions.
上個月被派了幾個工項,
其中一個是解我們開單員拍到的車牌照片。
由於我們開單員同仁都是阿伯阿桑,
基本上不太會用 PDA 拍照,所以拍回來的照片都歪歪的。
不太像場站固定機位會回傳的那樣方正,有時候還會有部份缺漏。
為了解這個問題,我去研究過阜爾(城市車旅)、普客(Times)還有一些第三方怎麼做的?
至少到 2024 年這個時間點,停車場業者主要都是控制他們的開單員要拍正,
據我所知沒有任何一間廠商對這點做妥善處理。
先限縮一下問題,因為特徵點根據不同狀況有不同參照物,
通常車牌特徵點都是用角點,所以先把特徵點設定為角點。
解這個問題的關鍵有三個:
第一個是角點濾波器,你要怎麼知道抓出來的特徵點是不是角點?
第二個是角點的順序,
角點順序對了,就能做些線性代數運算把車牌校正回來再送去 OCR。
第三個是角點的缺補,有時候缺了一點就不能把車牌校正回來。
或是你只有對角兩點,要怎麼把這些點補回來?
這篇分享很幸運的狀況 – 四個角點都抓到,只需求其順序:
我有看過幾種校正角點的方法,
比較主流且技術樓地板低的方法是訓練車牌校正模型,
餵一堆歪斜的車牌讓機器模型幫忙校正、得出被校正後的四點座標。
比較聰明一點的會用四象限去分點位,
但是四象限法會遇到一些問題像是:
有重複點在同一象限,你要怎麼辦?
要比 X 軸 還是比 Y軸?
答案是先看在哪個象限,再寫邏輯處理。
有些人會說:
用霍夫變換抓直線回來校正車牌,不就可以把車牌四點都分到獨立的象限嗎?
我當初也是這麼想的,
但實務上會被水箱護網、環境因素(排水溝蓋等)帶歪,
請記得我們不是在做機臺 AOI 那種環境相對單純的工作,所以霍夫變換的效果有限。
所以用四象限法不僅會面臨邏輯複雜,
如果加了霍夫變換,又需要面臨霍夫變換的不穩健性。
結論:你應該用更好的方法!
Ray Casting法
這套是我自己有天看到 Carmack 的德軍總部為了節省計算量時用了 Ray Casting 後,
被 Ray Casting 啟發想出來的。
原理是利用任一從原點出發的向量,作為參考向量。
隨後計算每個點到原點的向量,稱為特徵向量,
將特徵向量與標準向量做 COS 值並計算角度,
為了保證角度要是同一個順序(順逆時鐘)求出來的,
最後記得看一下 COS 值正負做處理。
這套的好處相比於前述方法有三個:
1.是根據物理原理,這個順序一定是對的,
2.少去複雜的邏輯設計,程式碼易讀易於維護。
3.N個點的 Case 只須計算 N次,計算複雜度低。
 |
| Ray Casting 法 |
最後埋個彩蛋,參考向量設{-1, 0}能有效降低實務上的計算複雜度,
歡迎同行交流。
以上。
Please feel free to contact me if you have any questions.