本文建議有點雲特徵的先驗知識者閱讀,
我會盡量講得平易近人,
但仍建議請先參考此篇,先了解基本點雲處理如何處理特徵。
這篇論文的重點在於改變了底層特徵方法。
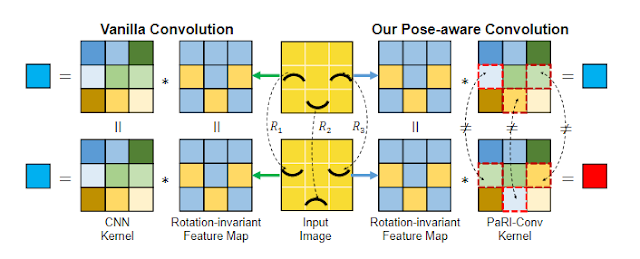
論文中由這張圖來解釋:
因為現行解決 Rotation Invariant 的方法都是乘上一個矩陣去收集數據,
並沒有考慮點與點之間的結構關係(i.e.上圖笑臉)。
但是我覺得這個例子呈述得很容易誤導,
聽起來很像在解決高低解析度、上下採樣的問題,
實際上在點雲裡面應該是解決類似 KNN 特徵的問題才對。
像是那三個有黑色像素的點,間隔距離、彼此夾角之類的結構關係所產生的資訊。
作者認為現在的 CNN 都沒有抓到結構關係 (Pose) 的精華
(e.g. 點雲中點與點的區域關係 AKA 底層特徵),
所以要提出解決方法稱為 PaRI 的新架構來解決問題
(我猜是 Pose: Ambiguity-free 3D Rotation-invariant 的縮寫)。
舊有的底層特徵方法:
好,那要改進一定得知道改哪裡嘛?
之前別人是怎麼做這種結構特徵的?
答案是:Point Pair Feature(PPF)
 |
| Point Pair Peature |
Pr 是參考點,想像成 KNN 的目標點;
Pj 是 Pr 附近的鄰居點,有 K 個;
∂n_r 是相較於 r 的三維座標軸,用 gram-schmidt orthogonalization 算出來的,
忘記的同學可以去複習一下 GSO。
所以經過 PPF 計算,我們會得到一組四個特徵如下圖:
這樣會出個小問題,各位想想好的底層特徵應該要具備什麼特性?
應該要具備獨特性嘛!
因為這樣訓練起來才不會與其他特徵混淆。
仔細觀察 αn 的方程式我們會發現,沒有一條能分辨在這個半徑為 d 的圓圈上,
有若干個法向量相同的 Pj 的辦法。
(∂1_r, ∂1_j 分別代表各自的法向量,ModelNet40資料集會給定。)
改善方法:
在改善之前,我們先想想舊有方法遇到什麼問題?
問題是缺少 Pr 與 Pj 間的獨特特徵,對吧?
所以我們希望新的方法最好讓每個 Pj 對 Pr 有獨特性。
Local Reference Frame(LRF) + Augmented Point Pair Feature(APPF)
就能解決這個問題。
LRF
 |
| Local Reference Frame |
左邊那個飛機圖,是為了說明使用 Global Feature 會有問題而存在的,
有興趣可以深入論文研究。
LRF 這裡我們要先建三軸,首先要拿到 e^2_r;
e^2_r = Pr – mr 的座標向量,mr 是 Pj 們的重心。
接著根據公式建三軸:
APPF
 |
| Augmented Point Pair Feature |
接著把 d 投影到 π_d 上。
什麼?你說 π_d 是什麼?
論文這裡沒有寫得很清楚,
我也看了很久,最後是對照著官方程式碼看才看出來。
其實 π_d 就是座標向量 e^2_r!
投影上去,然後用 arctan 取角度回來。
不知道為什麼用 arctan 而不用 tan 的同學,這裡有兩個理由:
1.對應域
i.e. tan(45°) = 1 = tan(225°)
但是 arctan 只會給你 45°
2.極值
tan(89.9°) ≈ 5729.58,但 tan(90.1°) ≈ -5729.58。
arctan(5729.58) ≈ 89.9°,但 arctan(-5729.58) ≈ -90.1°。
以上。
若有任何錯誤請聯絡我xD