前陣子在咱們一群影像愛好者的群組開始流傳一套程式,
一套號稱能檢測愛情動作片封面詐欺的程式!
什麼?天底下有這等好事?
於是我找到了開發這套程式的仁兄要到了原始論文,
認為他實現得不夠完美,間接促使我完成這項服務。
這篇文章可以幫你得出一個修圖參考值
(但某些情況不適用,文後會補充說明。)
接著會介紹論文以及背後數學原理,
對於檢測服務比較有興趣可以直接跳到後面。
原理
本文是 Analyzing Benford’s Law’s Powerful Applications in Image Forensics 這篇論文的延伸應用:
要講解這篇論文就要先解釋什麼是 Benford’s Law?
Benford’s Law 的概念就是人類世界中隨機數其實並不隨機,
其中數據的首位數字是遵循某種規律,這個規律就是 Benford’s Law。
Benford’s Law 公式:
$F_a = log_{10}{(frac{a+1}{a})}$, for all a = 1,2,…,9
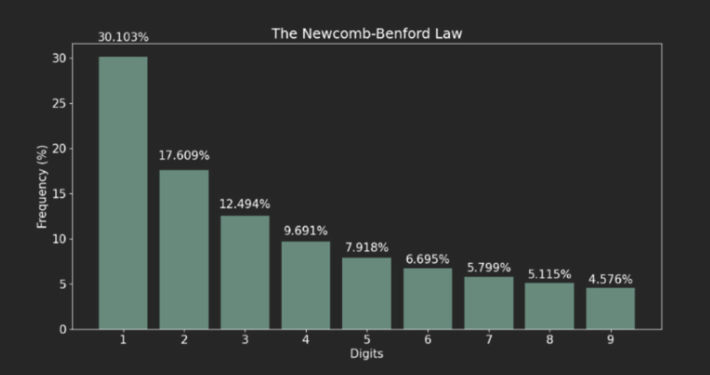
這樣算起來會呈現由首位數字出現比率是 1 往 9 遞減的一個分佈:
舉個 Benford’s Law 的例子,
如果他們沒有說謊的話,這一萬人的存款首位數字應該會符合 Benford’s Law。
而論文本意是拿這個結論做二次壓縮來估測 JPEG 的壓縮率,
有興趣的大家可以自己閱讀一下論文。
實作
$C(u) =
begin{cases}
frac{1}{sqrt{2}}, & text{if } i = 0 \
1, & text{otherwise}
end{cases}$
$C(v) =
begin{cases}
frac{1}{sqrt{2}}, & text{if } j = 0 \
1, & text{otherwise}
end{cases}$
身為一個影像從業者,
一定要做到比內建函式庫快!
俗話說得好:
要看一個人會不會做立委,就要看他怎麼做立委。
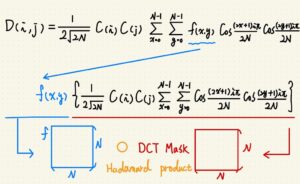
我是說要加速就要從數學看起,所以讓我們來看一下公式:
其中 $D(i, j)$ 是轉換後的值,$i, j$ 是位置參數;
$f(x, y)$ 是原始圖片的亮度值,$x, y$ 也是位置參數。
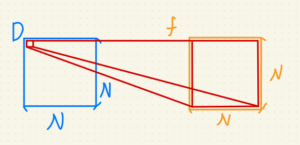
發現亮度值可以提出來,其中位置參數可以自己組一個矩陣相乘,
我們暫且把包含所有 $i, j$ 組合的稱為母矩陣。
這個母矩陣可以重複用,就不用每個區塊都要算。
(原始圖片會被 N*N 的小區塊分割,N 通常是 8。)
因為一組 $i, j$ 負責一組子矩陣,
所以如果輸出入尺寸相同,母矩陣大小為: $N * N * N * N$
於是我用這方法寫了一個 Mask 法,
的確速度與 OpenCV 內置函數比肩了,但是還沒有超越(#。
再加速
於是我又對平行運算生起了一絲邪念,
如果我宣告一組共享記憶體紀錄首位數字,
並對計算每個區塊的計算採取平行運算呢?
起初我是用 Lock 方法,後來發現這樣設計寫入的時候會有 Race Condition 問題,
後來便採取 Lock free 實作,缺點是佔用的記憶體較多。
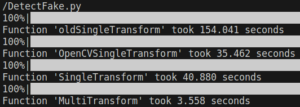
oldSingleTransform 為單執行緒的土法煉鋼法(公式法),
SingleTransform 及 MultiTransform 則分別為 Mask 的 單執行緒、多執行緒方法。
數據判讀
本人拿自己的相片去做測試,發現若是原圖進去做計算,
目前線上提供服務的機器人都是使用 DownSample 方法做計算。
特別需要說明的是手機原生相機就會做白平衡、明暗部校正,
尤其是 iPhone 做得非常優秀。
所以如果整張調亮/暗的偵測不出來。
開源
係數有正負,為了避免計算途中正負相減過小(float32 小數點後有效七位),
而把值歸零所以加入的。
原始論文使用 Uncompressed Colour Image Database 資料庫,
探討使用原始無損圖片如何估計 JPEG 壓縮率,
所以本文的物理意義是估算原始無損圖片與輸入圖片的差異度。
本文估計值僅供參考,
窮盡科技之力後不如鼓起勇氣約網戀對象出來走走!