快速排序算法擁有最佳計算複雜度 O(n log n),
但在特殊情況下會退化成 O(n^2)。
其中一個特殊情況就是大量重複元素的排列問題。
解決問題前,
先介紹快速排序法的實現。
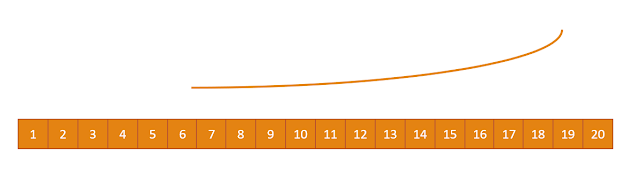
假設你得到一隨機一維陣列要做升冪排序,
最終的結果需要是這樣:
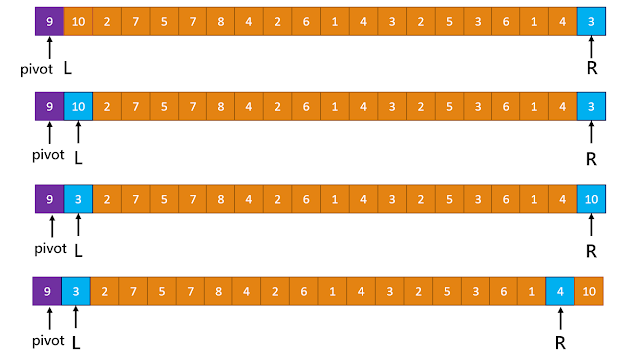
選定隨機陣列最左側為 pivot ,pivot 為 L指標、最右側為 R指標。
首先先判斷終止條件:R 的 index 是否等於 L 的 index?
等於的話就將 pivot 的 值 與 R、L 的值交換,進行下一循環。
R 的 index 不等於 L 的 index的話繼續尋找:
R指標啟動尋找小於等於 pivot 的值,L 尋找大於 pivot 的值,找到就鎖定。
若 R 的 index != L 的 index,則兩者的值交換。
以此類推,當 R 的 index == L 的 index 時,交換 pivot 與 R 的值。
並以交換點為準,分割左邊右邊兩個子循環。
這邊可以順便推導為什麼 quick sort 的計算複雜度為 O(n log n),
因為相較於 bubble sort 中每個 pivot 要比較 n-1 個元素,
quick sort 在第二次以後的理想狀況每個 pivot 只需比較 (n/2)^m個元素
(m=排序次數-1)。
所以最佳計算複雜度才會是 O(n log n) // n個 pivot 乘上該次比較元素量。
但是齁,人算不如天算。
有時候就會遇到很棘手的情況,讓 quick sort 一點都不 quick。
主要分為兩種:
- 已排序數列。
- 存在著大量重複元素的數列。
1.已排序數列。
已排序數列的問題在於分割的左右子陣列不平衡,
導致需要搜尋的元素趨近於 n。
如此一來計算複雜度便會退化成 O(n^2)
解法:把數列打亂即可解決這個問題。
2.存在著大量重複元素的數列。
這個就比較麻煩了,因為打亂也解決不了(#。
這個問題在於要搜尋相等於 pivot 的重複數,
兩數之間總共有三種關係嘛:大於、等於、小於。
之前的方法一直把等於的方法掛在 L指標上面做,
解決問題的核心精神是特別考慮等於的情況處理。
重複數處理範例:
令 pivot 為最左側的 index,L的 index 等於 privot +1,R 的 index 為最右側的 index。
一樣先判斷 L 有沒有大於 R?
沒有的話 L 先搜尋,分為三種情況:
1.L中的元素比 privot 還要小:
L 與 pivot 交換元素。
privot++
privot++
L++
2.L中的元素等於 privot :
L++
3.L中的元素大於 privot :
檢查 R元素
R元素 大於 pivot:
R–
R元素 等於 pivot:
L元素 與 R元素交換
R–
L++
L++
R元素 小於 pivot:
L元素 與 R元素交換
R–
L元素 與 pivot交換
L元素 與 pivot交換
privot++
L++
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <iostream<
#include <vector<
#include <algorithm<
#include <random<
void swap(int *array, int i, int j) {
array[i] = array[i] ^ array[j];
array[j] = array[i] ^ array[j];
array[i] = array[i] ^ array[j];
}
void quicksort(int *array, int left, int right) {
if (left >= right)
{
return;
}
int P = left;
int L = left;
int R = right;
while(L <= R)
{
if(nums[L] < nums[P])
{
swap(nums, L, P);
L++;
P++;
}
else if(nums[L] == nums[P])
{
L++;
}
else
{
if(nums[R] > nums[P])
{
R--;
}
else if(nums[R] == nums[P])
{
swap(nums, R, L);
swap(nums, L, P);
R--;
L++;
}
else
{
swap(nums, R, L);
swap(nums, L, P);
R--;
L++;
P++;
}
}
}
quicksort(nums, left, P-1);
quicksort(nums, P+1, right);
}
int main() {
int ARRAY_SIZE = 100;
int array[ARRAY_SIZE];
// 設定隨機種子
srand(time(0));
// 生成隨機一維陣列
for (int i = 0; i < ARRAY_SIZE; i++) {
array[i] = rand() % 11; // 生成 0 到 100 之間的隨機整數
}
printf("原始陣列:");
for (int j = 0; j < ARRAY_SIZE; j++) {
printf("%d ", array[j]);
}
printf("n");
quicksort(array, 0, ARRAY_SIZE - 1);
printf("排序後:");
for (int j = 0; j < ARRAY_SIZE; j++) {
printf("%d ", array[j]);
}
printf("n");
return 0;
}
好,大功告成!
你現在可以用 Quick Sort 面對多重複元素的排列問題了!