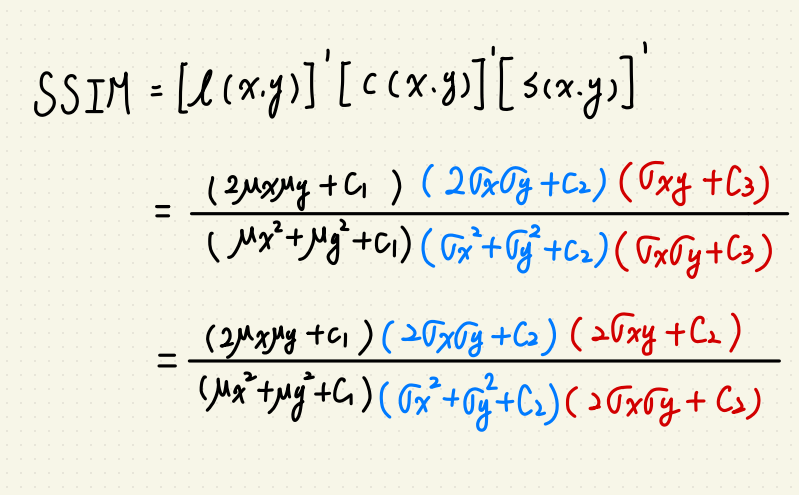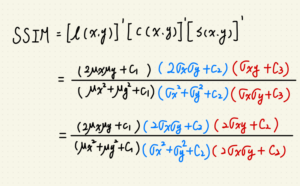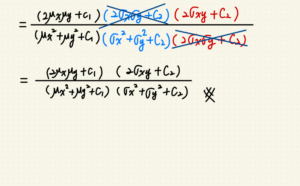SSIM 是一種指標,用於比較兩張圖的相異程度。
指標主要參考三個面向:
- 亮度 Luminance
$$l(xy) = frac{2mu_xmu_y+C1}{mu^2_xmu^2_y+C1}$$
- 對比度 Contrast
$$c(xy) = frac{2sigma_xsigma_y+C2}{sigma^2_xsigma^2_y+C2}$$
- 結構相似度 Structure
$$s(xy) = frac{sigma_{xy}+C3}{sigma_xsigma_y+C3}$$
以上的 $$C1 = K_1l^2, C2 = K_2l^2,C3 的部份可以簡化為 C3 = frac{C2}{2}$$
$$k_1 = 0.01, k_2 = 0.03, l 則為圖片的灰度值。$$
整體的 SSIM 為三項相乘:
$$SSIM(x,y) = [l(x,y)]^alpha[c(x,y)]^beta[s(x,y)]^gamma$$
在這邊 $$alpha, beta, gamma $$ 都簡化為 1。
這樣我們就可以簡化 SSIM 為:
然後我看到其他人有用 Numpy 實現,
就想著是不是自己能寫一版 PyTorch 來用?
大概會遇到兩個問題:
1.手刻 Gaussian Kernel 要塞在哪?
2.轉換資料至 GPU 上的時候會有誤差。
第一個問題當然是不能用 torch.nn.Conv2d() 來解,
因為這個 API 不能自己定義 Kernel,而且我們不希望這個 Kernel 的權重跑掉。
(Doc在此)
所以我們要用 torch.nn.functional.conv2d
(Doc在此)
接著我們要手刻一下 Gaussian Kernel:
def gaussian_fn(M, std):
n = torch.arange(0, M) - (M - 1.0) / 2.0
sig2 = 2 * std * std
w = torch.exp(-n ** 2 / sig2)
return w
def gkern(kernlen=256, std=128):
"""Returns a 2D Gaussian kernel array."""
gkern1d = gaussian_fn(kernlen, std=std)
gkern2d = torch.outer(gkern1d, gkern1d)
return gkern2d
這個方法我是從這邊看來的,
簡單來說就是從 1d Gaussian 用矩陣乘法造 2d Gaussian。
把整體程式碼寫出來:
def gaussian_fn(M, std):
n = torch.arange(0, M) - (M - 1.0) / 2.0
sig2 = 2 * std * std
w = torch.exp(-n ** 2 / sig2)
return w
def gkern(kernlen=256, std=128):
"""Returns a 2D Gaussian kernel array."""
gkern1d = gaussian_fn(kernlen, std=std)
gkern2d = torch.outer(gkern1d, gkern1d)
return gkern2d
def ssim_torch(img1, img2, kernel_size=11):
start_time = time.time()
C1 = (0.01 * 255)**2
C2 = (0.03 * 255)**2
transf = transforms.ToTensor()
guassian_filter = gkern(kernel_size, std=1.5).expand(3, 1, kernel_size, kernel_size)
H, W, C = img1.shape[0], img1.shape[1], img1.shape[2]
img1, img2 = torch.from_numpy(img1), torch.from_numpy(img2)
img1B, img1G, img1R = img1[:,:,0], img1[:,:,1], img1[:,:,2]
img2B, img2G, img2R = img2[:,:,0], img2[:,:,1], img2[:,:,2]
img1B, img1G, img1R = img1B.unsqueeze(0), img1G.unsqueeze(0), img1R.unsqueeze(0)
img2B, img2G, img2R = img2B.unsqueeze(0), img2G.unsqueeze(0), img2R.unsqueeze(0)
img1 = torch.cat((img1B, img1G, img1R), dim=0).unsqueeze(0).float()
img2 = torch.cat((img2B, img2G, img2R), dim=0).unsqueeze(0).float()
mu1 = F.conv2d(img1, weight=guassian_filter, stride=1, groups=3)
mu2 = F.conv2d(img2, weight=guassian_filter, stride=1, groups=3)
mu1_sq = mu1**2
mu2_sq = mu2**2
mu1_mu2 = mu1 * mu2
sigma1_sq = F.conv2d(img1**2, weight=guassian_filter, stride=1, groups=3) - mu1_sq
sigma2_sq = F.conv2d(img2**2, weight=guassian_filter, stride=1, groups=3) - mu2_sq
sigma12 = F.conv2d(img1 * img2, weight=guassian_filter, stride=1, groups=3) - mu1_mu2
ssim_map = ((2 * mu1_mu2 + C1) *
(2 * sigma12 + C2)) / ((mu1_sq + mu2_sq + C1) *
(sigma1_sq + sigma2_sq + C2))
print("This is torch_SSIM computer time: " + "{:.3f}".format((time.time()-start_time)))
return ssim_map.mean().detach().numpy()
這邊的 sigma_sq 是先把元素數量 N 提出來,
看起來有點不直覺要想一下。
如果你跟我一樣追求效率,就會想把 tensor.Tensor 轉成 tensor.Tensor.cuda 拿來加速。
這樣會遇到兩個小問題:
- 在單張圖片(2592 x 1520)下,轉成 tensor.Tensor.cuda 反而比較慢。
- 轉換後兩張相同圖片精度不是 1。
第一個小問題應該是轉換時間差,
第二個問題應該是 CPU 轉 GPU 的 tensor Loss。
結論:
- 在單張圖片下, PyTorch 版本的 SSIM 演算法速度會比 Numpy 快兩倍。
- 如果圖片不多,可以用 PyTorch(CPU) 轉比較快。
Ref.
https://stackoverflow.com/questions/60534909/gaussian-filter-in-pytorch
https://blog.csdn.net/a2824256/article/details/115013851
附上 Github Repo
如何對本文有任何疑問或書寫錯誤,
歡迎留言或是聯絡我:
wuyiulin@gmail.com
2023-11-13 分層捲積的更新
基於本部落格此篇文章的實現,
雖然寫得有點醜但親測可用!