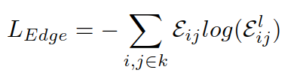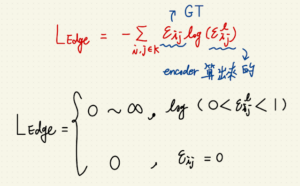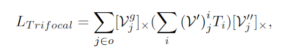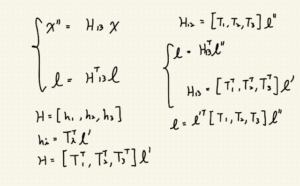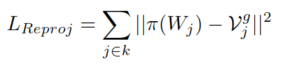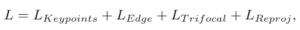這是一個很有趣的方法,以我的觀點來看是跟 3D 點雲的 Multi-View 方法的延伸。
主要是把 3D 點雲特徵用投影方法投回 2D 影像,
利用 2D/3D 的融合特徵解決物件遮蔽的偵測問題。
本篇數學推導較為艱澀,筆者在文中會推導重要部份。
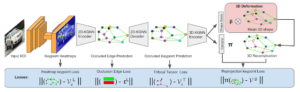 |
| 本文架構為四大 Loss值的組合。 |
L_Keypoints:
首先會先算 Keypoint Heatmaps,
從一台車裡面算出 12 個點對標資料集的 Keypoint GT。
(論文沒有細講,但個人從後面 KNN 猜測這裡做 L2 Norm。)
L_Edge:
在講 L_Edge 之前,我們要先定義 V 與 E:
大V 是由 k 個頂點組成的關鍵點集合,
而 V^l 代表 GT (真實的存在的關鍵點)、V^g 代表模型預測出來的關鍵點。
E_ij 代表點i 與 點j 組成的邊,若點i && 點j 皆屬於關鍵點,則 E_ij 為 1、其餘為 0。
把 V^g 還有 E_ij 拿去算三層的全連接層(FC)之後就會得到 E^l_ij。
這邊要特別注意 V^l 代表 GT,但是 E^l_ij 代表模型算出來的邊。
L_Edge 定義為:
(-1)* sigma * E_ij * log(E^l_ij)
L_Edge 的物理意義就是希望算出來的 E^l_ij 趨近於真實存在的 E_ij,
這邊應該還蠻 trivial 的。
L_Trifocal:
這個 Loss 就複雜很多,我們要談到多視角融合的原理。
首先我們要定義一個雙視圖:
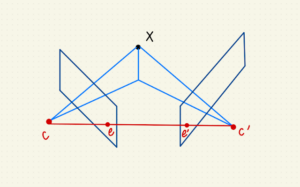 |
| 雙視圖解釋對極點 |
圖中 C 代表第一攝影機,C’ 代表第二攝影機。
第一視圖即是第一攝影機所看到的平面,第二視圖亦然。
第一視圖即是第一攝影機所看到的平面,第二視圖亦然。
e 點即是第二攝影機在第一視圖上所代表的點,
所以 e 點就是第二攝影機(C’ )對於第一攝影機(C)的對極點。
要算出攝影機對極點需要攝影機內置矩陣 K,
這個 K 矩陣牽涉基本矩陣 F,因為與本文較無關,筆者在此按下不表。
有興趣了解的朋友,筆者推薦:
“Multiple View Geometry in Computer Vision, 2/e, Richard Hartley” 一書
中興的學弟可以修資工所吳俊霖老師開的影像處理,
當年寫第一份作業就有寫到這部份。
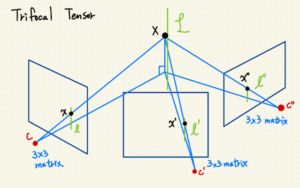 |
| 假設有三個攝影機照同一個 X點的三視圖 |
現在我們有了攝影機矩陣 P、P’、P”:
P = [ I | 0 ]
P’ = [ A | a_4 ]
P” = [ B | b_4 ]
a_i, b_i 代表攝影機矩陣的第 i 個 column。
(如參照中國資料,那邊會說 column = 列,與臺灣直行橫列剛好相反,須注意。)
以 P 當作觀察的攝影機來說,
a_4, b_4 在此代表 P’, P” 攝影機在 P攝影機平面的對極點。
讓 i 代表第i 個攝影機, a,b 代表非 i 的其他兩個攝影機,
那麼三焦張量 T_i 的定義就是:
T_i = (a_i)(b_4)^t – (a_4)(b_i)^t
所以 T 算出來應該要是 3x3x3 矩陣,可以自己推導一下。
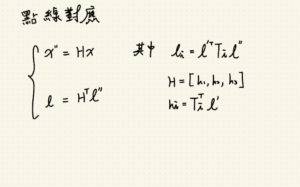 |
| 點線對應關係 |
接下來我們要用三個視圖中的點線對應關係推導三焦張量的損失,
兩關係式:
- x” = H_13 * x
- l = (H_13^t) * l”
x” 為空間中 X點在第三視圖上的投影,
H_13 矩陣實為第一視圖投影至第三視圖中的投影矩陣。
其中 H_13 = [h_1, h_2, h_3], h_i = T^t_i * l’。
根據空間中的關係又可以推導出:
H_12 = [T_1, T_2, T_3] * l”
暫時看不懂 H_12 怎麼來的沒關係,先知道就好。
因為 H_13 = [h_1, h_2, h_3], h_i = T^t_i * l’,
所以 l = (H_13^t) * l”
-> l = ([T_1, T_2, T_3]^t * l’)^t * l”
-> l = l’^t * [T_1, T_2, T_3] * l”
所以我們要複習一下大學線性代數 – 反對稱矩陣。
先定義反對稱矩陣:
任意矩陣 A 的反對稱矩陣 B 為 B = A^t – A,
反對稱矩陣的特性為 B^t = (-1)*B。
接著複習反對稱矩陣表達式:
Assume two martrix a, b,
a cross b == [a]x * b == (a^t * [b]x)^t.
又自己 cross 自己等於零,
零矩陣的轉置是不是也是零矩陣?
所以 0^t == [a]x * a == a^t * [a]x
沒錯!不要猶豫!
自信地把等式同乘 (-1)!
筆者高中時就是班上最自信的那位,自信地讓高中數學被當!
但是這裡真的可以同乘啦!
以上複習完畢。
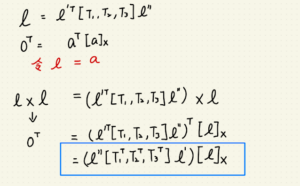 |
| 由線推導點的投影 – 1 |
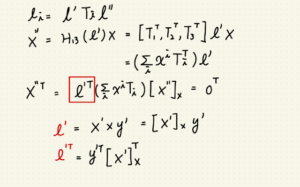 |
|
|
由點投影關係式 x” = H_13 * x 為基底推導,
由上一段可知 H_13 = [T^t_1, T^t_2, T^t_3] * l’,
則 x” = H_13 * x
-> x” = [T^t_1, T^t_2, T^t_3] * l’ * x
-> x” = sum(X_i * T^t_i) * l’
-> x”^t = l’^t * sum(X_i * T^_i)
由前段可知 a cross a 為零,所以:
x”^t * [x”]x == l’^t * sum(X_i * T^_i) * [x”]x == 0^t
接著我們要來拆解 l’,
x’為空間中 X 在第二視圖上的投影,令 y’ 為第二視圖上過 l’ 的任意點。
l’ = x’ cross y’ = [x’]x * y’
l’^t = y’^t * [x’]x^t
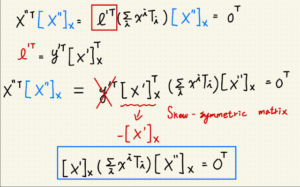 |
| 將 l’ 帶回等式 |
由前段可知 l’^t = y’^t * [x’]x^t,
將其帶回 l’^t * sum(X_i * T^_i) * [x”]x == 0^t
-> y’^t * [x’]x^t * sum(X_i * T^_i) * [x”]x == 0^t
由於 y 點可以為 l’ 上的任意點,所以 y’^t 可以消去,
此段在”Multiple View Geometry in Computer Vision, 2/e, Richard Hartley” 一書中有證明,
但為文章內容簡潔本文按下不表。
又可利用 skew-symmetric matrix 性質:
A^t = (-1)*A
所以
[x’]x^t = (-1)*[x’]x
推導最終結果為:
-> [x’]x *(sumx_i*T_i)*[x”]x = 0
與三焦損失相比較:
將不可視的模型預測點 V^g_j 與推導結果做 cross,
若完美預測,則 Loss 為零。
L_Trifocal 以上推導完畢。
L_Reproj:
這裡做 pi(W_j) 的物理意義是把 3D空間預測點座標圖投影回 2D平面,
特別注意 V^g_j 也是 2D平面的座標預測點。
Total Loss:
最後把四個 Loss 加總起來就可以了 ODO!
如何對本文有任何疑問或書寫錯誤,
歡迎留言或是聯絡我:
wuyiulin@gmail.com