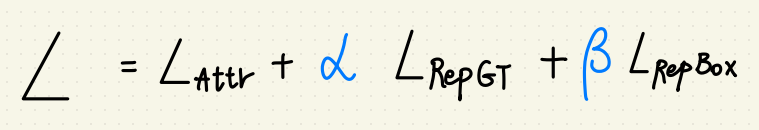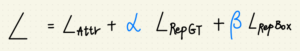最近小弟接到公司派的任務,
主要負責解決物件重疊的問題。
這篇算是我的物件重疊解法啟蒙之作,提筆紀錄一下。
Repulsion Loss 主要是作者看到磁力作動所併發的想法,
(這說法跟牛頓他老爺子被林檎砸到有 87%像)
- L_Attr – 使 BBOX_pred 與配對到的 GT BOX 相近。
- L_RepGT – 使 BBOX_pred 遠離其他 GT BOX 。
- L_RepBOX – 使 BBOX_pred_i 遠離預測其他出不同類別的 BBOX_pred_i,
可以避免因為距離太近,NMS 把框砍掉的問題。
(至於 NMS 機制可以看這篇,我認為他講得很好。)
Alpha 與 Beta 就有點 Focal Loss 的味道了,
兩數和被一所約束。
L_Attr
L_Attr 的物理意義是使預測的框(BBOX_pred)與配對到的 GT BOX 接近。
要算 L_Attr 就要先定義兩項集合:
{G} = 所有的 GT BOX 集合
{P} = 所有正樣本的 Anchor 集合
這裡簡單解釋一下 {P},就是所有包含前景的 Anchor 們,
或是所有有物件、不是背景的 Anchor 們集合。
這邊我也疑惑了一下什麼正樣本,有 BBOX 不就代表有物件了嗎?
接下來用 G, P 集合造 G^P_Attr:
G^P_Attr = argmax_G∈G IOU(G, P)
這個意義在於讓偵測到物件的每個 Anchor 都有一個家(GT BOX)。
但是 G^P_Attr 畢竟還是一個對應關係,
一個是 Anchor 、一個是 BBOX 還是不能算 Loss,
所以利用 P 去做 B^P,也就是基於 P 的 BBOX。
接著用 L1_Smooth 造 L_Attr:
L_Attr 結案!
L_RepGT
L_RepGT 的物理意義是使預測的框(BBOX)遠離其他不屬於自己的 GT BOX。
要算 L_RepGT 也要先求一個 G^P_Rep ,
G^P_Rep 的物理意義是:
對於該 BBOX_pred 來說 IOU 第二大的 GT BOX(最有機會的外遇對象)。
我們為了阻止 BBOX_pred 外遇(#,
所以把 G^P_Rep 算出來之後拿去與 B_P 做 IOG,
再給它一個重疊度太高的懲罰權重。
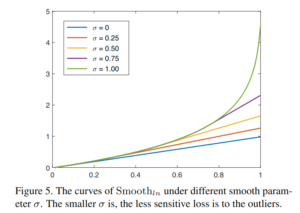
至於這邊為什麼是用 Smoothln 而不是 SmoothL1
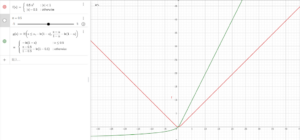 |
| 綠色為Smoothln; 紅色為 SmoothL1; |
以下個人猜測:
因為 IOG 的值域是 0-1,越趨近於 1 ,Loss 應該要越大。
Smoothln 看起來比 SmoothL1還好調整懲罰權重(調整 Alpha),
而且驗證 IOG 會不會出錯的時候也比較好用。
至於 Alpha 作為一個超參, Alpha 的值與對 outlier 的敏感度成正比。
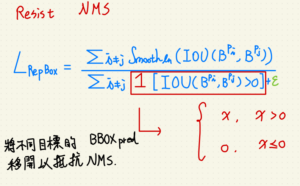
L_RepBOX
這個 Loss 就比較直覺,主要提一下 1,想像成乘上步階函數,把小於零的地方除值。
比較不同的是 x 為零時的定義為零。
比較不同的是 x 為零時的定義為零。
至於 epsilon 則是一個不為零的極小值,
目的是為了抵抗分母為零造成數值 NaN 的梯度爆炸問題。
目的是為了抵抗分母為零造成數值 NaN 的梯度爆炸問題。
以上,大概講一下我對於 Repulsion Loss 的理解。
如果有問題歡迎聯絡我:
wuyiulin@gmail.com